МАТЛАБ. ОПТИМІЗАЦІЯ, ЛІНІЙНЕ ПРОГРАМУВАННЯ.
Пошук екстремуму функції однієї змінної. Пошук локального (в межах певного інтервалу) мінімуму здійснює функція [x, y] = fminbnd (імяФункціі, граніциІнтервала). Якщо ж треба знайти локальний мінімум, то досліджувану функцію беруть з іншим знаком і шукають її мінімум, який фактично є її максимумом. При цьому значення функції в максимумі це знайдене значення з іншим знаком.
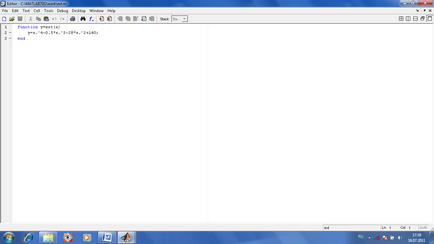
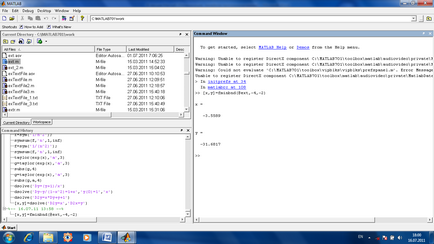
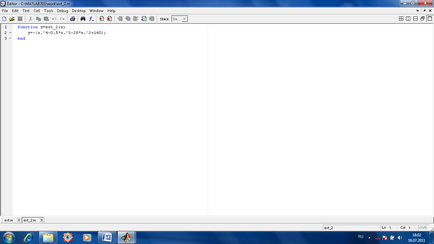
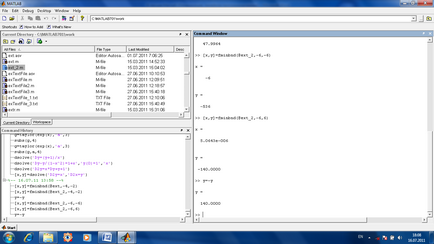
Пошук екстремуму функції кількох змінних. Якщо функція обчислюється від декількох змінних, то для пошуку її мінімуму використовується (після приблизної оцінки початкових наближень змінних в передбачуваному мінімумі) команда [x, y] = fminsearch (імяФункціі, векторНачальнихПрібліженійПеременних).
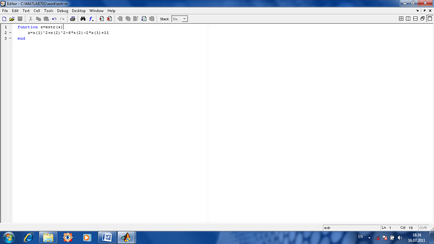
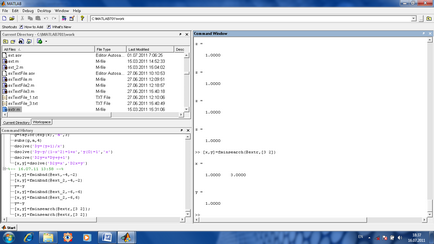
Рішення задач лінійного програмування. У завданнях лінійного програмування потрібно знайти максимум або мінімум лінійної функції багатьох змінних при лінійних обмеженнях у вигляді рівностей або нерівностей. Розглянемо для прикладу таку задачу.
Нехай функція L (x1, x2, x3, x4) = x1 + x2 + x3 + x4 і треба знайти її максимум і відповідні її максимуму значення змінних.
Нехай дано обмеження у вигляді нерівностей. x1 ≥0, x2 ≥0, x3 ≥0, x4 ≥0.
Нехай також дані ще обмеження у вигляді нерівностей.
Для вирішення завдання лінійного програмування (знаходження мінімуму) використовується функція [x, L, f] = linprog (c, A, b, A1, b1, Lx, Rx) де
x вектор значень змінних, отриманий в якості відповіді; L значення функції в мінімумі;
f параметр, що характеризує обчислювальний процес (якщо він нуль то рішення призупинено після досягнення максимального числа ітерацій, якщо позитивний то все нормально вирішено, якщо від'ємний то рішення не знайдено);
c функція мети представлена у вигляді вектора коефіцієнтів (в нашому випадку [1 1 + 1 -1] але так як нам потрібен максимум, а функція [x, L, f] = linprog (c, A, b, A1, b1, Lx, Rx) шукає мінімум, то у виразі для функції поміняємо знак, тому вектор коефіцієнтів буде [-1 -1 -1 1]);
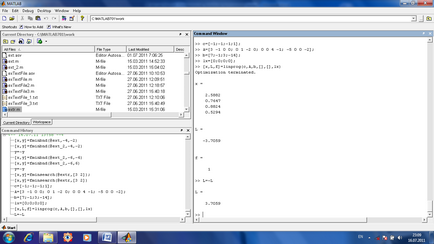
A, b система обмежень, задана в матричному вигляді Ax≤b (це в нашому завданні обмеження 3x1 -x2 ≤7, x2 -2x3 ≤-1, 4x3 -x4 ≤3, 5x1 + 2x4 ≥14, але так як 5x1 + 2x4 ≥14 не підходить, то треба поміняти знак у цьому нерівності і тоді воно буде -5x1 -2x4 ≤-14, в такому випадку матриця а складається з коефіцієнтів (при змінних) в цих нерівностях, а стовпець b складається з правих (що не містять змінних ) частин нерівностей;
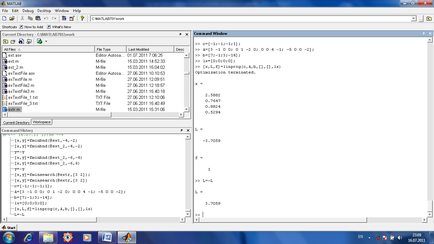
A1, b1 система рівності виду A1x = b (в нашому завданні такої системи обмежень немає, але могла б бути);
Lx, Rx відносяться до обмежень у вигляді Lx≤x≤Rx, Lx≤x, x≤Rx (в нашому завданні є обмеження виду Lx≤x, тому вектор Lx буде 0 0 0 0).
При використанні функції linprog в списку аргументів замість тих, які не вказані, ставляться порожні квадратні дужки.
Розглянемо ще приклад для тренування. Нехай дана функція W = x1 + x2 + 3x3 -x4 і треба знайти її максимум. Нехай дано обмеження у вигляді нерівностей.
Вирішимо задачу за допомогою функції [x, L, f] = linprog (c, A, b, A1, b1, Lx, Rx). Для її застосування нам треба підготувати аргументи функції. Вектор з коефіцієнтів функції дорівнює (1 + 1 3 -1 +), але так як функція linprog шукає мінімум, а нам потрібен максимум, то поміняємо знак біля коефіцієнта функції і тоді вектор з буде (-1 -1 -3 1). Матриця А складається з коефіцієнтів при змінних в системі нерівностей x1 -5x2 + 4x3 ≤5, x1 -2x2 -3x3 ≤4, x1 + 6x2 + 5x3 ≤4, x2 + x3 ≤1. Так як всі вони зі знаком ≤ то нічого змінювати не потрібно. Вектор b складається з правих частин цих же нерівностей. Матриця A1 з системи A1х = b1 для нас не актуальна (немає таких умов). Lx, Rx відносяться до обмежень у вигляді Lx≤x≤Rx, Lx≤x, x≤Rx. У нас є обмеження у вигляді нерівностей. x1 ≥0, x2 ≥0, x3 ≥0, x4 ≥0. Тоді вектор Lx = [0; 0; 0; 0]. Що стосується інших типів обмежень, то так як у нас немає таких обмежень, то для нас вони не важливі.
Завдання нелінійного програмування. Нелінійна задача відрізняється від лінійної. У ній є система лінійних нерівностей Ax≤b, система лінійних рівностей A1x = b1, система обмежень виду lx≤x≤rx, lx≤x, x≤rx. Однак крім цих вже знайомих (з лінійного програмування) умов, є ще система нелінійних обмежень виду g1 (x) ≤0, і система нелінійних рівності g2 (x) = 0. Для вирішення задачі нелінійного програмування (після вибору вектора початкових наближень х0) використовується функція [x, y, f] = fmincon (F, x0, A, b, A1, b1, Lx, Rx, G), де G це М-функція , що обчислює ліві частини нелінійних обмежень g1 (x) ≤0, g2 (x) = 0. Якщо якісь аргументи не визначені, то замість них у виклику функції ставляться квадратні дужки.
Розглянемо для прикладу таку задачу. нехай дана функція x1 2 + x2 2 = 1 за умови, що x1 x2 = 4, x1 ≥0, x2 ≥0. Вектор початкових наближень приймемо рівним х0 = (0.1, 0.1).