Магічний. або чарівний квадрат - це квадратна таблиця, заповнена n 2 числами таким чином, що сума чисел у кожному рядку, кожному стовпці і на обох діагоналях однакова. Якщо в квадраті рівні суми чисел тільки в рядках і стовпцях, то він називається полумагические. Нормальним називається магічний квадрат, заповнений цілими числами від 1 до n 2. Магічний квадрат називається асоціативним або симетричним. якщо сума будь-яких двох чисел, розташованих симетрично щодо центру квадрата, дорівнює n 2 + 1.
Нормальні магічні квадрати існують для всіх порядків, за винятком n = 2. хоча випадок n = 1 тривіальний - квадрат складається з одного числа. Мінімальний нетривіальний випадок показаний нижче, він має порядок 3.
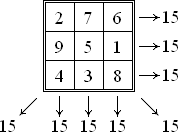
Сума чисел в кожному рядку, стовпці і на діагоналях, називається магічною константою. M. Магічна константа нормального чарівного квадрата залежить тільки від n і визначається формулою
Перші значення магічних констант наведені в наступній таблиці (послідовність A006003 в OEIS):
Сума чисел на будь-який горизонталі, вертикалі і діагоналі дорівнює 34. Ця сума також зустрічається у всіх кутових квадратах 2 × 2, в центральному квадраті (10 + 11 + 6 + 7), в квадраті з кутових клітин (16 + 13 + 4 + 1 ), в квадратах, побудованих «ходом коня» (2 + 8 + 9 + 15 і 3 + 5 + 12 + 14), в прямокутниках, утворених парами середніх клітин на протилежних сторонах (3 + 2 + 15 + 14 і 5 + 8 + 9 + 12). Більшість додаткових симетрій пов'язано з тим, що сума будь-яких двох центрально симетрично розташованих чисел дорівнює 17.
Квадрати Генрі Е. Дьюдени і Аллана У. Джонсона-мл.
Якщо в квадратну матрицю n × n заноситься не строго натуральний ряд чисел, то даний магічний квадрат - нетрадиційний. Нижче представлені два таких магічних квадрата, заповнені в основному простими числами. Перший має порядок n = 3 (квадрат Дьюдени); другий (розміром 4x4) - квадрат Джонсона. Обидва вони були розроблені на початку двадцятого століття [6]:
Є ще кілька подібних прикладів:
Останній квадрат, побудований в 1913 р Дж.Н.Мансі, примітний тим, що він складений з 143 послідовних простих чисел за винятком двох моментів: залучена одиниця, яка не є простим числом, і не використано єдине парне просте число 2.
Квадрати з додатковими властивостями
Диявольський магічний квадрат
Диявольський магічний квадрат - магічний квадрат, в якому також з магічною константою збігаються суми чисел по ламаним діагоналях (діагоналі, які утворюються при згортанні квадрата в тор) в обох напрямках.
Такі квадрати називаються ще пандіагональних.
Існує 48 диявольських магічних квадратів 4 × 4 з точністю до поворотів і відображень. Якщо взяти до уваги ще й їх додаткову симетрію - торичні паралельні переноси, то залишиться тільки 3 істотно різних квадрата:
Побудова магічних квадратів
Ще простіше побудова виконати наступним чином. Береться матриця n x n. Усередині її будується ступінчастий ромб. У ньому осередку зліва вгору по діагоналях заповнюються послідовним поруч непарних чисел. Визначається значення центрального осередку C. Тоді в кутах магічного квадрата значення будуть такими: верхня права клітинка C-1; нижня ліва комірка C + 1; нижня права комірка C-n; верхня ліва комірка C + n. Заповнення порожніх клітинок в східчастих кутових трикутниках ведеться з дотриманням простих правил: 1) по рядках числа зліва направо поступово збільшуються на n + 1; 2) за стовпцями зверху вниз числа збільшуються з кроком n-1.
Також розроблені алгоритми побудови пандіагональних квадратів, [14] [15] як втім і пандіагональних і асоціативних магічних квадратів 9x9. [16] [17] Ці результати дозволяють будувати ідеальні магічні квадрати порядків n = 9 (2k + 1) для. [9] [18] Існує також загальний метод компонування ідеальних магічних квадратів непарного порядку n> 3. [19] Розроблено метод побудови ідеальних магічних квадратів порядку n = 8k, k = 1,2,3. [20] пандіагональних квадрати парному-непарного порядку вдається скомпонувати лише в тому випадку, якщо вони нетрадиційні. [21] [22] [23]. Проте, можна знаходити майже пандіагональних квадрати [24] Знайдена особлива група ідеально-скоєних магічних квадратів (традиційних і нетрадиційних) [25].
Приклади більш складних квадратів
Методично суворо відпрацьовані магічні квадрати непарного порядку і порядку подвійний парності. [26] Формалізація квадратів порядку одинарної парності набагато важче, що ілюструють такі схеми:
Існують кілька десятків інших методів побудови магічних квадратів
шаховий підхід
Відомо, що шахи. як і магічні квадрати, з'явилися десятки століть тому в Індії. Тому невипадково виникла ідея шахового підходу до побудови магічних квадратів. Вперше цю думку висловив Ейлер. Він спробував отримати повний магічний квадрат безперервним обходом коня. Однак, це зробити йому не вдалося, оскільки в головних діагоналях суми чисел відрізнялися від магічної константи. Проте шахова розбивка дозволяє створювати будь-магічний квадрат. Цифри заповнюються регулярно і через підрядник з урахуванням кольору осередків.
Зображення схем побудови магічних квадратів.