Скалярним добутком векторів і називається число, яке дорівнює добутку довжин цих сторін на косинус кута між ними.
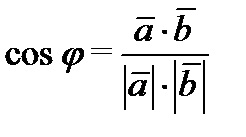
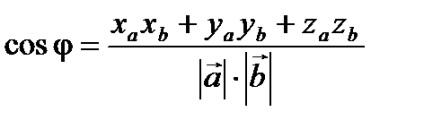
Якщо вектори задані в координатної формі. ,
то їх скалярний добуток обчислюється за формулою:
Властивості скалярного твори:
Векторний добуток векторів. Властивості. Застосування.
Векторним твором векторів і називається вектор. задовольняє таким умовам:
1). де j - кут між векторами і.
2) вектор ортогональний векторам і
3). і утворюють праву трійку векторів.
Властивості векторного добутку векторів
5) Якщо задані вектори в декартовій прямокутній системі координат з одиничними векторами. то
-орт осей координат Ox, Oy, Oz, відповідно:
6) Геометричним змістом векторного добутку векторів є площа паралелограма, побудованого на векторах і. .
Зауваження: якщо потрібно відняти площу паралелограма, то потрібно порахувати спочатку,
Змішане твір векторів. Властивості. Застосування.
Змішаним твором трьох векторів
Змішане твір має такі властивості:
1). якщо всі три вектора паралельні одній і тій же площині (компланарність);
2) циклічна перестановка
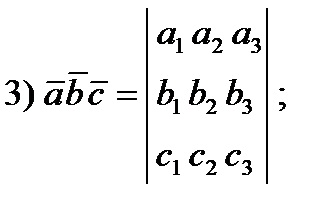
4) обсяг паралелепіпеда, побудованого на векторах і. дорівнює
якщо a * b * c> 0, то трійка a, b, c - права, якщо a * b * c<0, то тройка a,b,c - левая
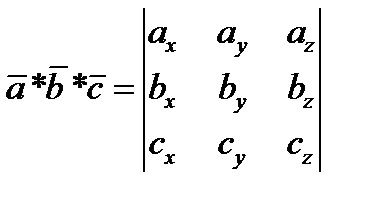
Умова компланарності 3х векторів.
Векторний базис. Координати вектора. Розкладання вектора по базису.
Базис - група в-в ч / з котор висловлюють все лин простір. У 3хмерном Простягни-ве базис складається з 3х некомплан-нихв-в. В пл-ти 2 в-ра.
Ортогональний базис складається з взаімноперпендік-нихв-в. ()
Нормований базис складається з одиничних століття-рів ().
За замовчуванням беруть ортогональний базис.
Розкладання по базису:
-проекції або коорд в-ра.
13.Условія коллинеарности, ортогональности, компланарності векторів.
Умова ортогональності векторів
Два вектора ортогональні за умови рівності нулю їх скалярного твори:
Умова коллинеарности векторів
Якщо вектори колінеарні (лежать на одній прямій або напараллельних прямих) тобто кут між ними або 0, або 180 0. то їх векторний добуток дорівнює нулю:
Умова компланарності векторів
Вектори компланарні (розташовані в одній площині), якщо їх змішане твір дорівнює нулю:
Лінійні оператори. Власні значення і власні вектори лінійного оператора. Лінійні моделі обміну.
над полем P, є лінійний оператор, якщо
1) для будь-яких векторів
2) для будь-якого вектора і будь-кого.
Власні вектори і власні значення лінійного оператора.
1) Матриця лінійного оператора:
нехай # 966; -Л.О. векторного простору V над полем P і один з базисів V:
нехай
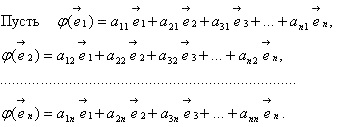
Тоді матриця Л.О. # 966 ;:
2) Зв'язок між матрицями лінійного оператора в різних базисах:
M (# 966;) - матриця Л.О. # 966; в старому базисі.
M1 (# 966;) - матриця Л.О. # 966; в новому базисі.
Т - матриця переходу від старшого базису до нового базису.
2) Дії над лінійними операторами:
нехай # 966; і f - різні Л.О. векторного простору V.
тоді # 966; + f - сума лінійних операторів # 966; і f.
k · # 966; - множення Л.О. на скаляр k.
# 966; · f - твір лінійних операторів # 966; і f.
Являюіся також Л.О. вектороного простору V.
4) Ядро лінійного оператора:
d (# 966;) - розмірність ядра Л.О. # 966; (Дефект).
5) Образ лінійного оператора:
ran # 966; - ранг Л.О. # 966; (Розмірність Jm # 966;).
6) собсвенно вектори і власні значення лінійного вектора:
# 61623; нехай # 966; - Л.О. векторного простору V над полем P і і
Якщо то # 955; - власне значення
- власний вектор Л.О. # 966 ;, що відповідає # 955 ;.
# 61623; Характеристичне рівняння Л.О. # 966 ;:
# 61623; Безліч власних векторів, що відповідають власному значенню # 955 ;:
# 61623; Л.О. вектороного простору називаються Л.О. з простим спектром, якщо # 966 ;, якщо # 966; має рівно n власних значень.
# 61623; якщо # 966; - Л.О. з простим спектром, то він має базис з власних векторів, щодо якого матриця Л.О. # 966; діагональна.