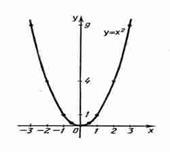
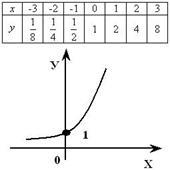
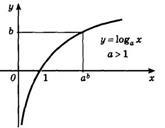
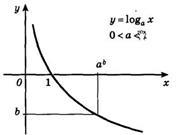
4. Графік логарифмічної функції завжди проходить через точку (1; 0).
5. Зростаюча логарифмічна функція, буде позитивною при x> 1, і негативною при 0<х<1.
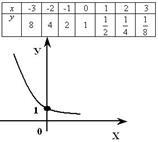
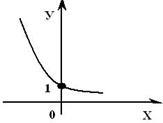
На наступному малюнку представлений графік спадної логарифмічною функції - (0
7. Функція не є парній або непарній. Логарифмічна функція - функція загального вигляду.
8. Функція не має точок максимуму і мінімуму.
Область визначення функції-безліч Rвсех дійсних чисел. Безліч значень функції - відрізок [-1; 1], тобто синус функція - обмежена. Функція непарна: sin (-x) = - sin x для всіх х ∈ R. Графік функції симетричний відносно початку координат. Функція періодична з найменшим позитивним періодом 2π. sin (x + 2π · k) = sin x, де k ∈ Z для всіх х ∈ R. sin x = 0 при x = π · k. k ∈ Z. sin x> 0 (позитивна) для всіх x ∈ (2π · k. π + 2π · k), k ∈ Z. sin x <0 (отрицательная) для всех x ∈ (π+2π·k. 2π+2π·k ), k ∈ Z.
Функція зростає від -1 до 1 на проміжках:
Функція убуває від -1 до 1 на проміжках:
- При x 0 - графік залишається без змін,
- при x <0 — график симметрично отражается относительно оси ординат.
21)) Сукупність чисел, кожне з яких забезпечено своїм номером п (п = 1, 2, 3.), називається числовою послідовністю.
Окремі числа послідовності називаються її членами і позначаються зазвичай так: перший член a1. другий a2. п -й член an і т. д. Вся числова послідовність позначається
22) Арифметична прогресія. Числова послідовність, кожен член якої, починаючи з другого, дорівнює попередньому, складеному з постійним для цієї послідовності числом d, називається арифметичною прогресією. Число d називається різницею прогресії. Будь-член арифметичної прогресії обчислюється за формулою:
Сума n перших членів арифметичної прогресії обчислюється як:
Геометрична прогресія. Числова послідовність, кожен член якої, починаючи з другого, дорівнює попередньому, помноженому на постійне для цієї послідовності число q. називається геометричній
прогресією. Число q називається знаменником прогресії. Будь-член геометричної прогресії обчислюється за формулою:
Сума n перших членів геометричної прогресії обчислюється як:
Нескінченно спадної геометричною прогресією називається нескінченна геометрична прогресія, знаменник якої задовольняє умові.
При необмеженому зростанні сума перших членів нескінченно спадної геометричної прогресії прагне до числа. яке називаетсясуммой нескінченно спадної геометричної прогресії.
) Похідна функції f (x), f '(x). сама є функцією. Значить, можна знайти eё проізводную.Назовём f '(x) похідної функції f (x) першого порядка.Проізводная від похідної функції f (x) називається похідною другого порядку (або другої похідної).
Геометричний зміст похідної. Похідна в точці x 0 дорівнює кутовому коефіцієнту дотичної до графіка функції y = f (x) в цій точці.
Рівняння дотичної до графіка функції: y = f (a) + f '(a) (x - a) y = f (a) + f' (a) (x - a)
Фізичний зміст похідної. Якщо точка рухається вздовж осі х і її координата змінюється за законом x (t), то миттєва швидкість точки:
24)) Похідна суми (різниці) функцій
Похідна алгебраїчній суми функцій виражається наступною теоремою.
Похідна суми (різниці) двох диференційовних функцій дорівнює сумі (різниці) похідних цих функцій:
Похідна кінцевої алгебраїчної суми функцій, що диференціюються дорівнює такій же сумі алгебри похідних доданків. наприклад,
Схожі статті