Опр1. Вектор, називається базисом на прямий L, якщо вектор, || L може бути записаний у вигляді
Опр2.Два лінійно незалежних вектора, що лежать в площині P, називаються базисом на площині Р, якщо вектор, що лежить на площині Р можна записати у вигляді.
Опр3.Трі лінійно незалежних вектора називаються базисом в просторі, якщо вектор може бути записаний у вигляді
1. Будь-який ненульовий вектор, утворює базис на прямій L.
2. Будь-яка пара неколінеарних векторів, що лежать в площині Р утворює базис на площині Р
3. Будь-яка трійка некомпланарих векторів утворює базис в просторі.
(2) на площині
(3) в просторі
Опр4 Праві частини формул (1), (2), (3) називаються розкладанням векторів по базису; ; відповідно, числа відповідними координатами.
Теорема1: Розкладання по базису єдино (самостійно!)
Теорема2: При додаванні векторів їх відповідні координати складаються. При множенні вектора на число його координати множаться на це число
18. Проекція вектора на вісь. Декартова система координат. Напрямні косинуси.
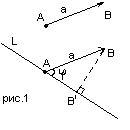
Опр1: Вектор називається векторною проекцією вектора на вісь L.
Опр2: скалярні проекцією вектора на вісь L величину:
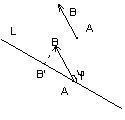
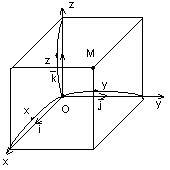
Зафіксуємо Т.О. Розглянемо трійку i, j, k. (I ^ j) = (i ^ k) = (j ^ k) =; | i | = | j | = | k | = 1; т.О - загальна початкова точка. Вектор i визначає вісь Ох, j - вісь Oy, k- вісь Oz.
Тим самим ми ввели Декартову систему координат в пространстве.Пусть т. М - довільна точка. Добудуємо прямокутний паралелепіпед з діагоналлю ОМ.
Довжини ребер | x |, | y |, | z |. Координати Т.М - речові числа x, y, z;
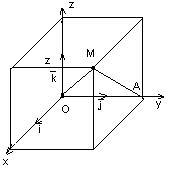
Затвердження: Декартові координати точок збігаються зі скалярними проекціями вектора на відповідні осі:
- прямокутний; y = OA = | | Cos = | | Cos =
Аналогічно для x і z.
Опр: Величини,, називаються напрямними косинусами вектора.
Розділимо обидві частини рівняння на
19. Скалярний добуток векторів і його властивості.
Определние: Величина (a, b) = | a | * | b | * cos (a ^ b) називається скалярним пр-ем векторів a і b. Очевидно, що можна записати (a, b) = | a | * (проекція b на а) і навпаки.
Властивості скалярного твори:
4) (a, a) ≥0, причому (a, a) = 0, коли a = 0.
(A, b + c) = | a | * (проекція (b + c) на a) = | a | * (проекція b на а) + | a | * (проекція c на а) = (a, b) + (a, c) .Скалярное твір дорівнює 0 тоді і тільки тоді, коли a перпендикулярно b, або a = 0, або b = 0.
20. Векторний добуток векторів і його властивості. Необхідна і достатня умови коллинеарности векторів.
Определние: Вектор c називається векторним добутком векторів a і b, позначається c = [a, b], якщо | c | = | a | * | b | * sin (a ^ b), c перпендикулярний a і b, abc- права трійка.
Властивості векторного твори:
Лемма a = b ó для будь-якого d (a, d) = (b, d)
- Кінець роботи -
Ця тема належить розділу:
Опр Матрицею A розмірності Sxn називається прямокутна таблиця з чисел складається з S рядків і n стовпців. елемент матриці.