Якщо у гіперболи збігаються дійсна і уявна піввісь, тобто a = b, то кут між асимптотами дорівнює 2arctg (b / a) = 2arctg1 = π / 2, тобто є прямим. Таку гіперболу називають равнобочной. Для неї крім канонічної системи координат, в якій осі координат збігаються з осями симетрії гіперболи, розглядають також і іншу, осями якої є асимптоти. Виведемо рівняння гіперболи в цій системі координат, яку позначимо Oxy. Нехай i, j - її репер. а i ', j' - репер канонічної системи координат Ox'y '(рис. 8.1).
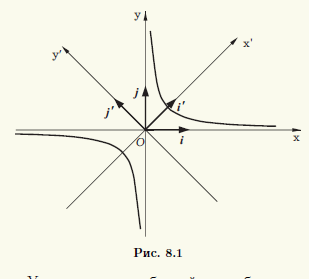
Канонічна система координат повернута відносно системи Oxy на кут π / 4. Тому (див. 4.2) i '= √2 / 2i + √2 / 2j, j' = -√2 / 2i + √2 / 2j Значить, координати x ', у' канонічної системи координат виражаються через координати x, у з тими ж коефіцієнтами: x '= √2 / 2x + √2 / 2у, y' = -√2 / 2x + √2 / 2у
Рівняння равнобочной гіперболи в канонічній системі координат має вигляд (x ') 2 - (у') 2 = a 2. де a - дійсна (вона ж хибна) піввісь гіперболи. Замінивши в цьому рівнянні канонічні змінні на x, у, отримаємо 1/2 (x + y) 2 - 1/2 (x - у) 2 = a 2. або
Рівняння (8.1) називають рівнянням гіперболи в асимптотами.
Зауваження 8.1. Рівняння xy = -a 2/2 задає пов'язану гіперболу для равнобочной гіперболи (8.1).
Приклад 8.1. Знайдемо координати вершин, фокусів і рівняння асимптот гіперболи xy = - 8 і побудуємо її.
Дане рівняння є рівнянням в асимптотами для сполученої равнобочной гіперболи. Тому осі координат, тобто прямі x = 0, у = 0, є її асимптотами. Для цієї гіперболи -a 2/2 = -8, тому a 2 = 16 і a = b = 4. Але тоді c = √ (a 2 + b 2) = √ (4 +2 +4 2) = 4√2, і, з огляду на позначення вершин і фокусів, знаходимо: A (-2√2; 2√2), B (2√2; - 2√2), F1 (-4; 4), F2 (4; -4) ( рис. 8.2).