




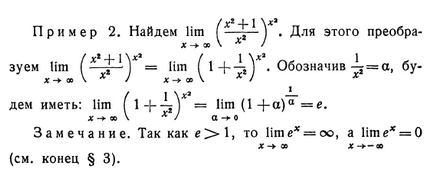
Властивості меж У всіх прикладах, які були наведені вище, ми не знаходили меж, а доводили, що таке-то число є межею заданої функції при вказаних умовах. Природно виникає питання, як знайти те число, щодо якого далі будемо доводити, що воно є межею заданої функції. Це завдання майже завжди є дуже важкою, особливо якщо виходити з визначення меж. Для полегшення цього завдання зазвичай використовують деякі властивості меж, до викладу яких ми і переходимо. Наведені властивості будуть пояснюватися на прикладах, а докази даватися не буде. Докази можна знайти в більш повних курсах, наприклад: Піскунов Н. С. «Диференціальне та інтегральне числення» або Тарасов Н. П. «Курс вищої математики». Властивість 1. Межа суми визначеного числа функцій дорівнює сумі меж кожної з цих функцій, т. Е. Lim [/ (*) + q> (*)] «Іш / (*) + lira. х - * - а х а х -а У формулюванні цієї властивості, так само як і в наступних, передбачається, що всі межі обчислюються при одних і тих же умовах. Приклад 1. Знайдемо lim
sin * t знаючи, що X про X Зауваження. У формулюванні властивості 1 говориться про суму, але оскільки різниця завжди можна записати у вигляді суми, то властивість 1 поширюється і на різниці. sin х-х * Приклад 2. Знайдемо межа lim -. X о * Так як = + хл), то, застосовуючи властивість 1, отримаємо шп lim Х - * - О * X - + Q L Л J Властивість 2. Межа функції, що зберігає одне і те ж значення, дорівнює цьому значенню. Це властивість формулюють і інакше: межа постійного дорівнює такого постійного. Приклад 3. Знайдемо межа lim [sin ** + cos * х]. i X - 2 Так як sin * x - \ - cos * x при будь-яких значеннях х дорівнює 1, то тут має місце випадок, коли функція зберігає постійне значення, тому lim [sin * х + cos * х] = 1. 1 £ - г Приклад 4. Знайдемо межа lim 7,5. Так як 7,5 посто- X
* -х янно і не залежить від х, то lim 7,5 = 7,5. X я Властивість 3. Межа твори двох функцій дорівнює добутку меж цих функцій. т-г е і про х * sin X 4 sin * X Приклад 5. Знайдемо межа lim -j-. X -> про х В прикладі 1 цього параграфа було показано, що lim - = 1, а в § 2, - що lim = 1. Застосовуючи X - + Q Х X - * - Q Х властивість 3, отримуємо х * sin х -f sin * х Yx * -f sin x sin x
\ Lim X - t. x9 + sin * sin *. t = lim --- lim - = 1.1 = 1. X -> Про X X Q X Хоча в формулюванні властивості 3 говориться тільки про дві функції, але цим же властивістю можна користуватися і при більшій кількості співмножників. п в і м 1 * Г4 (sin * -f- cos * х) sin дс! 0 Приклад 6. Знайти lim ---- L-. Це Вира L х J ються можна представити як добуток двох співмножників: [4 (sin1 х + cos * *)] і Застосовуючи властивість 3, отримаємо Застосуємо це ж властивість до першого співмножники, отримаємо lim [4 (sin * jc + cos2 x )] lim = XQX 0 * = lim 4 lim (sin * x + cos1 x) lim = 4 • И = 4. X - * x Властивість 4. Межа приватного двох функцій дорівнює, частці від ділення межі діленого на межу подільника за умови, що межа дільника не дорівнює нулю. х -4-2 Приклад 7. Знайдемо межа lim -. * T х 1 Так як lim (х + 2) = 4, lim (х - 1) = 1, то за властивістю 4 х ж х г маємо 1 * + 2 4 А lim -
= - = 4. x-t * -1 1 Якщо ж межа дільника дорівнює нулю, то межа приватного може дорівнювати будь-якого числа в залежності від діленого. Наведемо приклади. Ахт Приклад 8. Розглянемо межа lim -, де т-ціле X х число> 0. У цьому прикладі межа дільника дорівнює нулю, так як lim jce = lim х-lim x »limx = 0. XX - * • 0 X Про X про Розберемо можливі окремі випадки. Якщо / і = 1, то lim lim = a lim - • lim - = оо У «Y * х. X X 0 Х- * 0 А Х-> 0 Х- * 0 Л (див. Ін. 5 § 1, а пояснення знака оо в ін. 2 § 3). Якщо т = 3, то lim - = Іга а- а. х 'про Л ах Якщо т = 5, то lim - = lim АХ1 = a lim ХГ = 0. X О * X -► 0 х про Зауважимо, що відшукання межі приватного двох функцій в разі, коли межі і дільника і ділимо одночасно дорівнюють нулю, є завданням, найбільш часто зустрічається і теоретично однією з найважливіших. Але саме в цьому випадку властивість 4 не приносить користі. Властивість 5 (важлива властивість межі). Якщо точка М рухається як завгодно по осі Ох, наближаючись до точки Р як до своєї межі і точка Р не збігається з початком координат, то можливі тільки два випадки: 1) якщо Р має позитивну абсциссу, то точка М з деяких пір має також позитивну абсциссу; 2) якщо Р має негативну абсциссу, то і точка М у якійсь точці має негативну абсциссу. Звідси: Якщо межа не дорівнює нулю, то з деяких пір знаки межі і допредельних, величини збігаються. § 5. Межа lim (1 + • *) *. Число е X про 1 Розглянемо функцію (l + x) *. Якщо х прагне до нуля, то вміст дужки наближається до одиниці. Якщо х не дорівнює нулю, то і дужка не дорівнюватиме одиниці; при цьому, якщо х більше нуля, то дужка більше одиниці, якщо х менше нуля, то дужка менше одиниці. 1 Розглянемо lim (1 + х) х. Неясно, чому він буде рав- няться, так як при число, більше одиниці, зводиться в позитивну ступінь, а при л число, менше одиниці, зводиться в негативну ступінь. Однак можна показати, що ця межа існує. Це доводиться в докладних курсах. Число, рівне цієї межі, позначається буквою е. Таким чином, числом е називається lim (1 + лг) *. X про Число е є ірраціональним числом, його наближене значення дорівнює (з точністю до однієї тисячної) 2,718. Воно зустрічається в математиці настільки ж часто, як і число я. Виявилося дуже зручним взяти число е за основу логарифмів. Логарифми з основою е називаються натуральними логарифмами. Вони позначаються знаком In. Цими логарифмами користуються переважно в теоретичних питаннях. Приклад 1. Знайдемо Позначивши - • = х, матимемо, що при п - »- оо х -> - 0. Тому (X * 4 1 -). Для цього преобра-. * / Зуемое lim = lim ^ 1. Позначивши ^ = бу- дем мати: lim (\ - \ - \ Y = lim (1 + а) а = е. * Оо V х) а про Зауваження. Так як е> 1, то lim ех = оо, a lim ех = О X СО X (див. Кінець § 3).